Modelling microbial motion: the case of Chlamydomonas reinhardtii
CIBIO Centre for Integrative Biology
Author: Luca Pizzagalli
Supervisor: Prof. Gianluca Lattanzi
Academic year 2017/2018
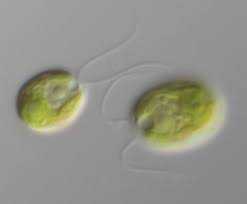
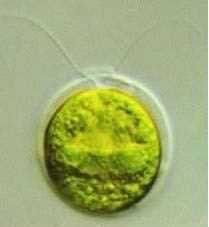
Chlamydomonas reinhardtii
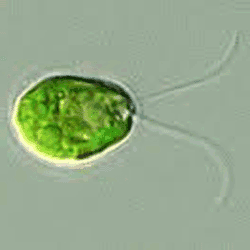
- Green algae, a single cell eukaryotic organism ≈10μm
- Model organism in biology, studied for photosynthesis and ciliary functions
- Possible source of useful proteins and bio-fuels
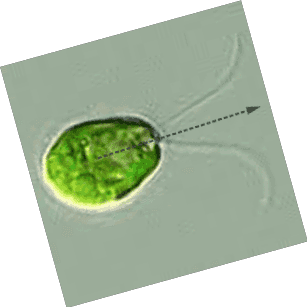
How does it move
- Puller micro-swimmer
- Breast-stroke motion
- Run and tumble:
straight swims alternated with rapid rotations
How to define a model for the motion of C. reinhardtii?
- Run and tumble motion
- Interaction with obstacles
- Results coherent with experiments
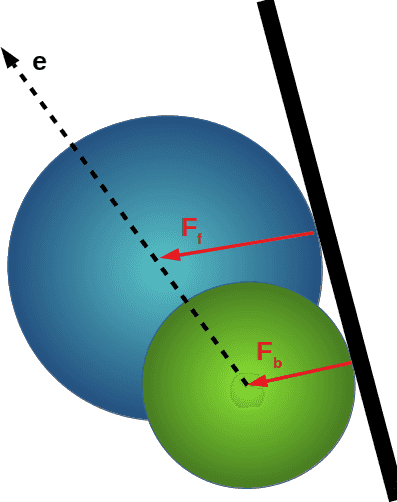
The Model
2D Asymmetric dumbbell, a sphere for the cell's body and a sphere for the area covered by the beating flagella

Equations of motion
dtdr(t)=v0e(t)+μF(r,e)+η(t)
⟨η(t)η(t′)⟩=2kbTμ1δ(t−t′)
Forces
F(r,e)=F(rb)+F(rf)
=−∇Ub(rb)−∇Uf(rf)
Truncated Lennard-Jones potential:
Ub(rb)=4ϵkbT[(∣rb−rw∣ab)12−(∣rb−rw∣ab)6]+ϵ
Uf(rf)=4ϵkbT[(∣rf−rw∣af)12−(∣rf−rw∣af)6]+ϵ
Direction
dtde(t)=(τT(r,e,t)+ξ)×e(t)
⟨ξz(t)ξz(t′)⟩=τp2kbTδ(t−t′)
Direction
Alternative expression, more useful for numerical computation
dtdϑ(t)=τTz(r,ϑ)+ξz(t)
Direction
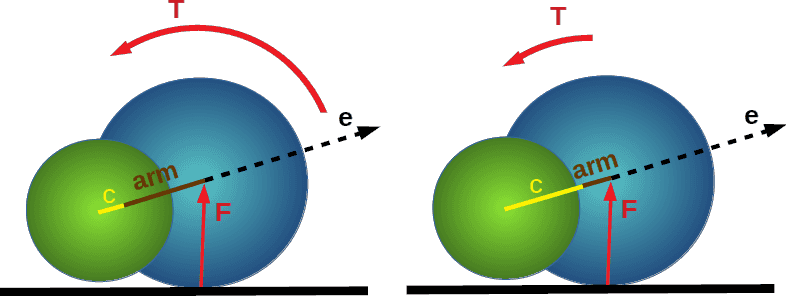
T(r,e,t)=Tb+Tf=−c(e×Fb)+(l−c)(e×Ff)
Tumble
T(r,e,t)=Tw(r,e)+Tt(t)
- Time between two tumbles: exponential distribution with average 11.2s
- Tumble duration: Gaussian distribution with average 2s
- Tumble strength: Gaussian distribution with average 0.75rad/s
Parameters
| variable |
|---|
| ab |
| aj |
| l |
| c |
| v0 |
| kbTμ |
| kbTτp |
| kbTτ |
| ϵ |
| μ[ts] |
| μ[τTt] |
| σ[τTt] |
| μ[tt] |
| σ[tt] |
| value | m. u. |
|---|---|
| 5.0 | μm |
| 7.5 | μm |
| 7.5 | μm |
| 0.0 | μm |
| 60−110 | μm/s |
| ?? | μm2/s |
| ?? | s |
| 0.15 | s |
| 10 | 1 |
| 11.2 | s |
| 0.75 | rad/s |
| 0.75 | rad/s |
| 2.0 | s |
| 1.5 | s |
Experimental Validation
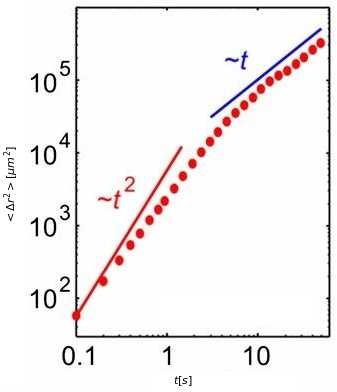
Mean square displacement from experiment in open space
- Short time: ballistic behavior
- Long time: diffusion behavior
Experimental Validation
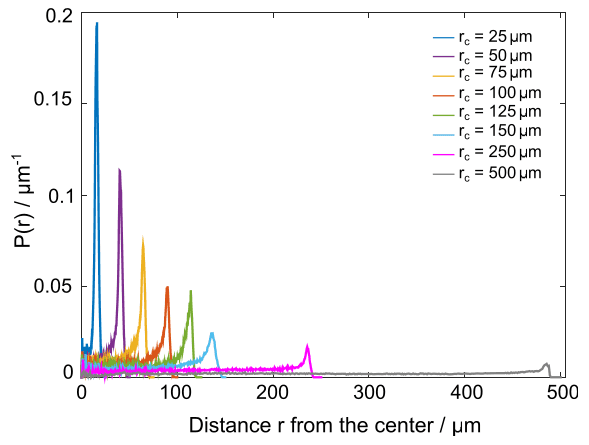
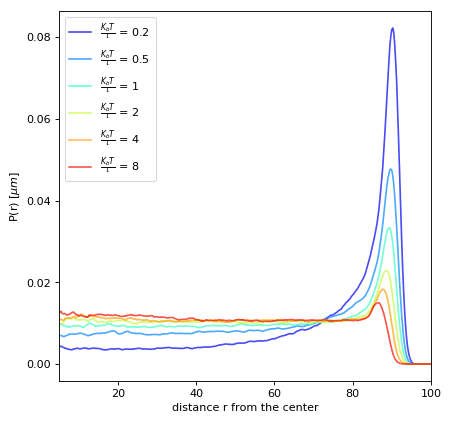
Radial probability P(r) in confined environment
P(r)=∫0R2πr′Δrh(r′)dr′2πrΔrh(r)
Numerical Simulation
Experiment
Experimental Validation
Experiment

Simulation
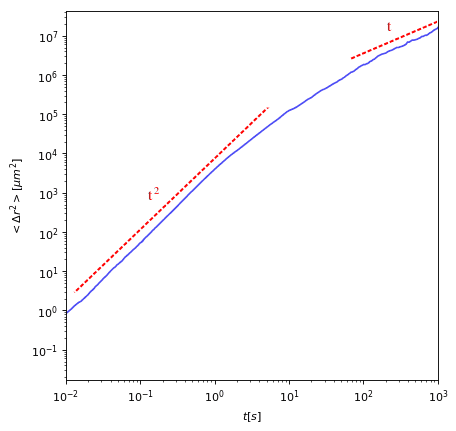
Experimental Validation
Experiment

Simulation
Parameters
| variable |
|---|
| ab |
| aj |
| l |
| c |
| v0 |
| kbTμ |
| kbTτp |
| kbTτ |
| ϵ |
| μ[ts] |
| μ[τTt] |
| σ[τTt] |
| μ[tt] |
| σ[tt] |
| value | m. u. |
|---|---|
| 5.0 | μm |
| 7.5 | μm |
| 7.5 | μm |
| 0.0 | μm |
| 10 | 1 |
| 70 | μm/s |
| 14 | μm2/s |
| 2.0 | s |
| 2.0 | s |
| 11.2 | s |
| 0.75 | rad/s |
| 0.75 | rad/s |
| 2.0 | s |
| 1.5 | s |
Dependence on parameters
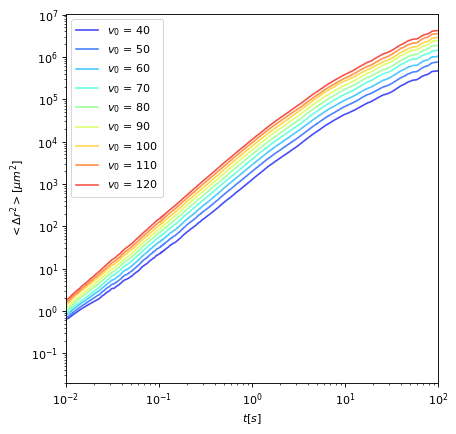
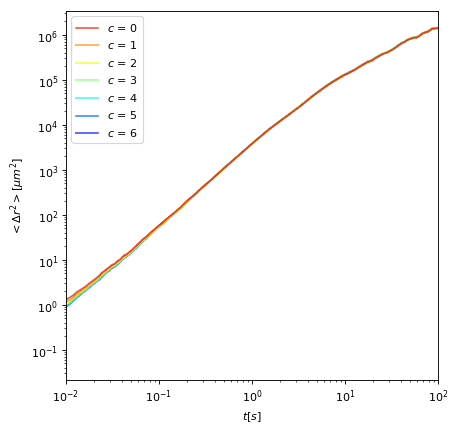
Propulsion Speed
Msd in open space
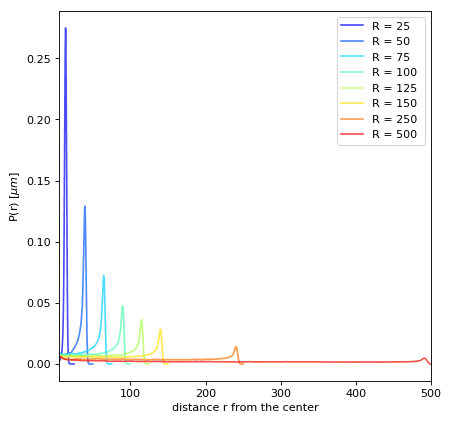
P(r) in confinement
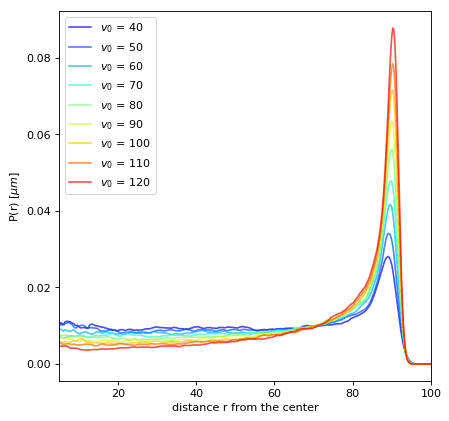
Rotational Axis
Msd in open space
P(r) in confinement
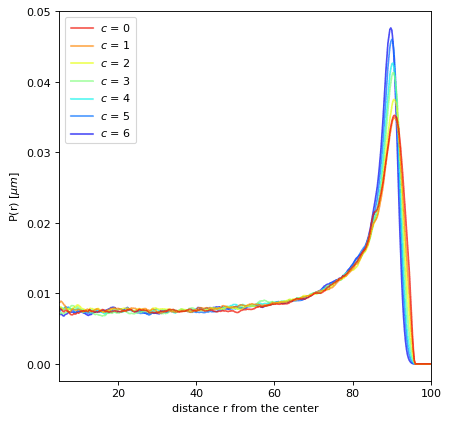
Rotational Axis
Tumble Strength
Msd in open space
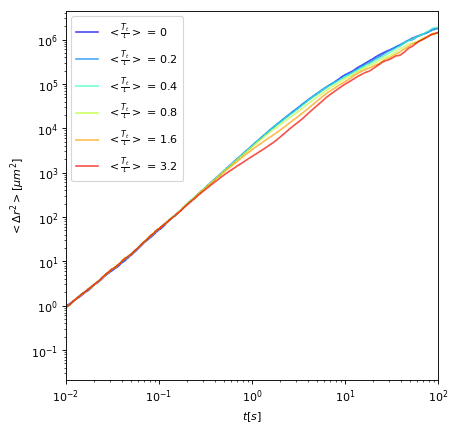
P(r) in confinement
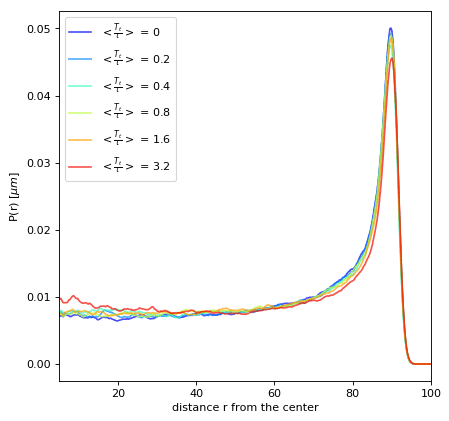
Translational Noise
Msd in open space
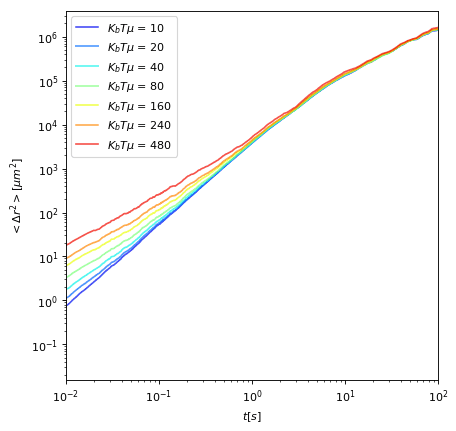
P(r) in confinement
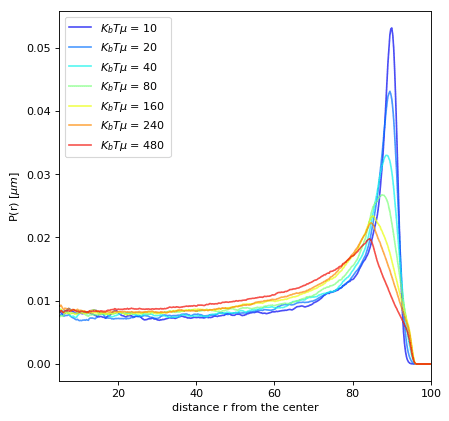
Rotational Noise
Msd in open space
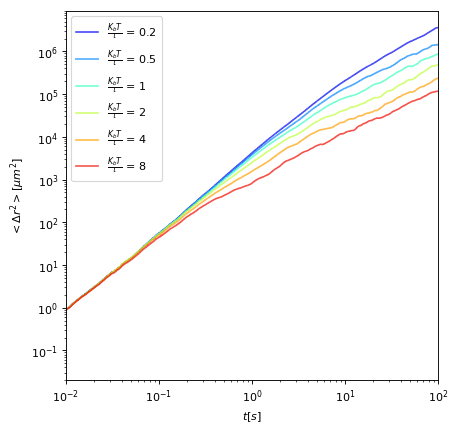
P(r) in confinement
Collective Behavior
Four components for the force:
F(r1,e1,r1,e2)=−∇Ubb(r1,b,r2,b)−∇Uff(r1,f,r2,f)−∇Ubf(r1,b,r2,f)−∇Ubf(r1,f,r2,b)
from truncated Lennard-Jones potentials
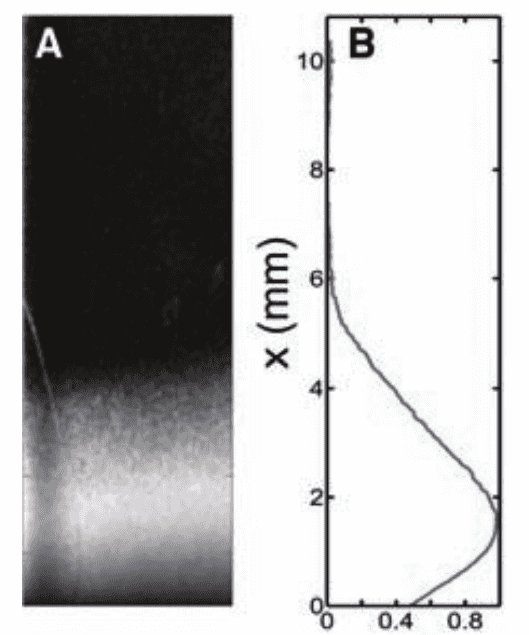
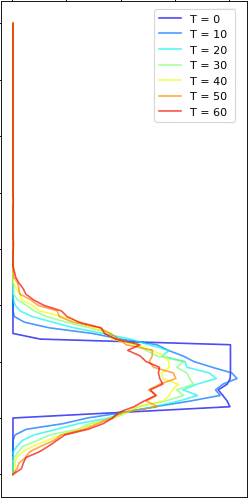
Diffusion
Linear density of a diffusion of C. reinhardtii in a test tube, 1 minute after centrifugation.
Experiment
Simulation
Conclusions
The model developed is powerful enough to reproduce:
- Ballistic and diffusive behavior in open space
- Long retention times when near convex walls
- Diffusion of cells in a suspension
Conclusions
The quantitative results are in good agreement with the experimental values, but:
- Some parameters are tuned to experiments
- Results show a significant dependence on the parameters used
Conclusions
Further extensions could take into account how the cell perceives the environment and modifies its behavior accordingly, including:
- Chemotaxis
- Gravitaxis
- Phototaxis